如何获取期权市场数据快照

来源：https://uqer.io/community/share/550274e4f9f06c7a9ae9a535

在本文中，我们将通过实际的市场的例子，展示如何在量化实验室中计算和展示期权的隐含波动率微笑。

import pandas as pd
from matplotlib import pylab
pd.options.display.float_format = '{:,>.4f}'.format

1. 获取市场数据

在本节中，我们使用数据API获取数据，并进行一些必要的数据转换。这里我们获取的是实时报价，是本 notebook 运行时的市场快照。

• dataDate 交易日
• dataTime 快照时间戳
• optionId 期权代码
• instrumentID 期权交易代码
• contractType 期权类型，CO为看着，PO为看跌
• strikePrice 行权价
• expDate 到期日
• lastPrice 最新价

optionSnapShot = OptionsDataSnapShot()
optionSnapShot[optionSnapShot.expDate == Date(2015,9,23)]

	dataDate	dataTime	optionId	instrumentID	contractType	strikePrice	expDate	lastPrice
30	2015-03-13	13:24:12	10000031	510050C1509M02200	CO	2.2000	September 23rd, 2015	0.3388
31	2015-03-13	13:24:17	10000032	510050C1509M02250	CO	2.2500	September 23rd, 2015	0.3019
32	2015-03-13	13:24:22	10000033	510050C1509M02300	CO	2.3000	September 23rd, 2015	0.2816
33	2015-03-13	13:24:27	10000034	510050C1509M02350	CO	2.3500	September 23rd, 2015	0.2484
34	2015-03-13	13:24:32	10000035	510050C1509M02400	CO	2.4000	September 23rd, 2015	0.2070
35	2015-03-13	13:24:36	10000036	510050P1509M02200	PO	2.2000	September 23rd, 2015	0.0690
36	2015-03-13	13:24:41	10000037	510050P1509M02250	PO	2.2500	September 23rd, 2015	0.0804
37	2015-03-13	13:24:47	10000038	510050P1509M02300	PO	2.3000	September 23rd, 2015	0.0955
38	2015-03-13	13:24:52	10000039	510050P1509M02350	PO	2.3500	September 23rd, 2015	0.1194
39	2015-03-13	13:24:58	10000040	510050P1509M02400	PO	2.4000	September 23rd, 2015	0.1322
46	2015-03-13	13:24:52	10000047	510050C1509M02450	CO	2.4500	September 23rd, 2015	0.1889
47	2015-03-13	13:24:58	10000048	510050P1509M02450	PO	2.4500	September 23rd, 2015	0.1555
54	2015-03-13	13:24:32	10000055	510050C1509M02500	CO	2.5000	September 23rd, 2015	0.1629
55	2015-03-13	13:24:36	10000056	510050P1509M02500	PO	2.5000	September 23rd, 2015	0.1900
62	2015-03-13	13:24:32	10000063	510050C1509M02550	CO	2.5500	September 23rd, 2015	0.1443
63	2015-03-13	13:24:36	10000064	510050P1509M02550	PO	2.5500	September 23rd, 2015	0.2169

2. 计算隐含波动率以及相关Greeks

接着我们可以方便的使用内置函数 BSMImpliedVolatity 计算期权的隐含波动率。

• price 市场报价或者模型价格
• delta 期权价格关于标的价格的一阶导数
• gamma 期权价格关于标的价格的二阶导数
• rho 期权价格关于无风险利率的一阶导数
• theta 期权价格关于到期时间的一阶导数（每日）
• vega 期权价格关于波动率的一阶导数

analyticResult = OptionsAnalyticResult()
analyticResult.loc[:10, ['optionId', 'contractType', 'strikePrice', 'expDate', 'lastPrice', 'vol', 'delta', 'gamma', 'rho', 'theta', 'vega']]

	optionId	contractType	strikePrice	expDate	lastPrice	vol	delta	gamma	rho	theta	vega
1	10000002	CO	2.2500	March 25th, 2015	0.2184	0.2259	0.9886	0.2947	0.0730	-0.0458	0.0133
2	10000003	CO	2.3000	March 25th, 2015	0.1730	0.2867	0.9165	1.1965	0.0687	-0.2996	0.0687
3	10000004	CO	2.3500	March 25th, 2015	0.1229	0.2177	0.8963	1.8495	0.0687	-0.2670	0.0806
4	10000005	CO	2.4000	March 25th, 2015	0.0814	0.2166	0.7676	3.1504	0.0596	-0.4503	0.1367
8	10000009	PO	2.3500	March 25th, 2015	0.0076	0.2482	-0.1332	1.9373	-0.0111	-0.3633	0.0963
9	10000010	PO	2.4000	March 25th, 2015	0.0159	0.2346	-0.2488	3.0197	-0.0207	-0.5061	0.1419
10	10000011	CO	2.2000	April 22nd, 2015	0.2778	0.2703	0.9081	0.7466	0.2152	-0.1661	0.1347

3. 构造波动率曲面

但是对于市场参与者而言，像刚才这样仅仅观察的线的结构不够。他们需要看到整个市场以到期时间，行权价为轴的波动率曲面（Volatility Surface）。除此之外，他们更想知道，波动率曲面上，那些并不是市场报价点的值，至少是个估计。这样的波动率曲面构造，往往需要依赖某种模型，或者某种插值方法。在这一节中，我们将介绍使用 CAL 中的波动率曲面构造函数。

以下的例子基于 CAL 函数: VolatilitySurfaceSnapShot

3.1 基于SABR模型的波动率曲面

volInterpolatorSABR = VolatilitySurfaceSnapShot(optionType = 'CALL', interpType = 'SABR')
volInterpolatorSABR.plotSurface(startStrike = 2.2,endStrike = 2.6)
volInterpolatorSABR.volalitltyProfileFromPeriods([2.2, 2.3, 2.4, 2.5, 2.6], ['1M', '2M', '3M', '6M', '9M'])

	1M	2M	3M	6M	9M
2.2000	0.2720	0.2406	0.2327	0.2531	0.2545
2.3000	0.2048	0.2207	0.2345	0.2546	0.2557
2.4000	0.2245	0.2341	0.2389	0.2525	0.2533
2.5000	0.2241	0.2328	0.2381	0.2479	0.2484
2.6000	0.2311	0.2356	0.2362	0.2425	0.2429

3.2 基于SVI模型的波动率曲面

volInterpolatorSVI = VolatilitySurfaceSnapShot(optionType = 'CALL', interpType = 'SVI')
volInterpolatorSVI.plotSurface(startStrike = 2.2,endStrike = 2.6)
volInterpolatorSVI.volalitltyProfileFromPeriods([2.2, 2.3, 2.4, 2.5, 2.6], ['1M', '2M', '3M', '6M', '9M'])

	1M	2M	3M	6M	9M
2.2000	0.2769	0.2476	0.2369	0.2566	0.2580
2.3000	0.2121	0.2223	0.2340	0.2535	0.2545
2.4000	0.2170	0.2292	0.2365	0.2504	0.2512
2.5000	0.2290	0.2357	0.2389	0.2474	0.2479
2.6000	0.2401	0.2417	0.2413	0.2508	0.2514

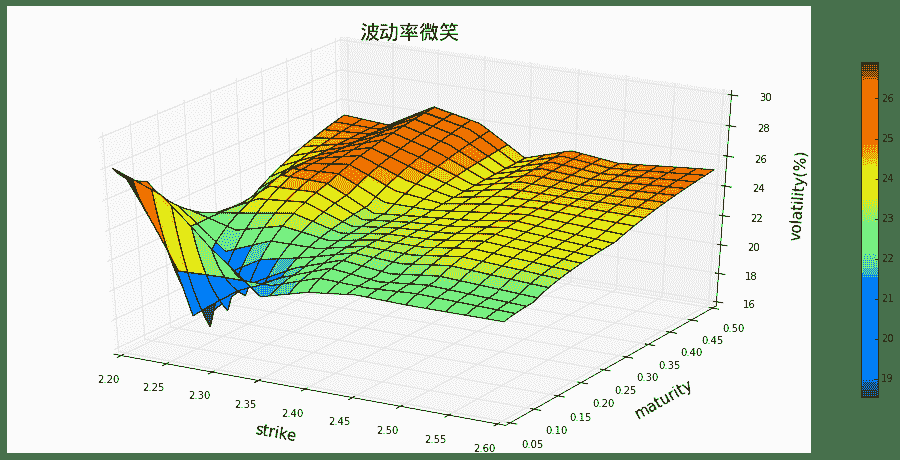
3.3 基于Balck波动率插值的波动率曲面

volInterpolatorVariance = VolatilitySurfaceSnapShot(optionType = 'CALL', interpType = 'BlackVariance')
volInterpolatorVariance.plotSurface(startStrike = 2.2,endStrike = 2.6)
volInterpolatorVariance.volalitltyProfileFromPeriods([2.2, 2.3, 2.4, 2.5, 2.6], ['1M', '2M', '3M', '6M', '9M'])

	1M	2M	3M	6M	9M
2.2000	0.2676	0.2380	0.2202	0.2516	0.2537
2.3000	0.2082	0.2270	0.2441	0.2660	0.2672
2.4000	0.2277	0.2325	0.2341	0.2404	0.2408
2.5000	0.2278	0.2363	0.2408	0.2463	0.2466
2.6000	0.2252	0.2324	0.2365	0.2517	0.2526

4. 组合计算

在本节中，我们假设客户已经拥有了自己的期权头寸，希望利用量化实验室的功能进行风险监控。我们假设有以下的期权头寸：

期权代码	数量	行权价（￥）	到期时间
10000004	-7000	2.35	2015-03-25
10000011	2000	2.20	2015-04-22
10000027	5000	2.25	2015-06-24
10000047	3000	2.45	2015-09-23

然后我们构造 OptionBook:

optionIDs = ['10000011', '10000027', '10000004', '10000047']
amounts = [2000, 5000, -7000, 3000]
optBook = OptionBook(optionIDs, amounts)
print u'期权头寸：'
optBook.description()

期权头寸：

	dataDate	dataTime	optionId	instrumentID	contractType	strikePrice	expDate	lastPrice	amount
0	2015-03-13	13:24:58	10000004	510050C1503M02350	CO	2.3500	March 25th, 2015	0.1229	-7000
1	2015-03-13	13:24:32	10000011	510050C1504M02200	CO	2.2000	April 22nd, 2015	0.2778	2000
2	2015-03-13	13:24:52	10000027	510050P1506M02250	PO	2.2500	June 24th, 2015	0.0450	5000
3	2015-03-13	13:24:52	10000047	510050C1509M02450	CO	2.4500	September 23rd, 2015	0.1889	3000

4.1 使用Black插值模型计算组合风险

optBook.riskReport(volInterpolatorVariance)

	optionId	vol	price	delta	gamma	rho	theta	vega
0	10000004	0.2060	-860.3000	-6370.8417	-12316.8687	-488.8540	1592.3418	-508.3851
1	10000011	0.2634	555.6000	1828.2807	1456.7054	433.8000	-307.9681	256.2961
2	10000027	0.2484	220.5000	-1103.5286	4552.0335	-831.0864	-856.2742	1945.3136
3	10000047	0.2509	566.7000	1659.5347	2626.2983	1876.5865	-503.9843	2135.1356
portfolio	NaN	nan	482.5000	-3986.5549	-3681.8315	990.4461	-75.8848	3828.3602

4.2 使用SABR模型组合风险

optBook.riskReport(volInterpolatorSABR)

	optionId	vol	price	delta	gamma	rho	theta	vega
0	10000004	0.2157	-865.4365	-6301.5462	-12703.7735	-483.0602	1800.8937	-549.0791
1	10000011	0.2523	552.8686	1845.2432	1405.9255	438.6890	-272.7679	236.9632
2	10000027	0.2347	194.1368	-1048.6009	4677.9921	-785.3771	-785.2668	1888.5079
3	10000047	0.2511	566.9933	1659.5667	2624.8517	1876.4726	-504.2584	2135.1279
portfolio	NaN	nan	448.5622	-3845.3372	-3995.0043	1046.7243	238.6007	3711.5199

4.3 使用SVI模型组合风险

optBook.riskReport(volInterpolatorSVI)

	optionId	vol	price	delta	gamma	rho	theta	vega
0	10000004	0.2126	-863.7639	-6323.4081	-12591.1718	-484.8898	1734.2876	-536.4362
1	10000011	0.2634	555.6000	1828.2807	1456.7054	433.8000	-307.9681	256.2961
2	10000027	0.2355	195.6318	-1051.9049	4670.9045	-788.1010	-789.3710	1892.0017
3	10000047	0.2495	563.6855	1659.2077	2641.2567	1877.7596	-501.1669	2135.2142
portfolio	NaN	nan	451.1534	-3887.8246	-3822.3052	1038.5689	135.7815	3747.0758

5 比较不同模型的拟合市场数据的能力

这里我们比较不同的模型，对于市场数据的拟合能力。这里我们可以观察到单论你和能力 BlackVarianceSurface > SviCalibratedVolSruface > SABRCalibratedVolSruface。这里我们并不想下这样的结论：这些模型的优劣也有相同的排序。

另一个我们可以观察到的现象，对于近月合约（流动性最好），波动率微笑是最规则的。在这个期限上，三种模型的拟合都很到位。随着期限的上升，流动性的下降，买卖价差也随之扩大。这时候波动率微笑变得愈发不规则，这个时候一个完美拟合至市场的模型是否必要，是一个很大的问题：如果市场报价并不理性，一个优秀的模型应该可以指出这种不合理点，而不是简单的接受市场的非理性。

from matplotlib import pylab

strikes = sorted(analyticResult['strikePrice'].unique())
expiries = [Date(2015,3,25),Date(2015,4,25),Date(2015,6,25),Date(2015,9,25)]
maturity = [(date - EvaluationDate())/ 365.0 for date in expiries]
volSurfaces = [volInterpolatorSABR, volInterpolatorSVI]

def plotModelFitting(index, volSurfaces, legends = ['Market Quote', 'SABR', 'SVI']):
    # Using Black variance surface to extrace the rar wolatility
    data = volInterpolatorVariance.volatility(strikes, maturity[index], True)
    pylab.plot(strikes, data, 'r+-.',  markersize = 8)
    for s in volSurfaces:
        data = s.volatility(strikes, maturity[index], True)
        pylab.plot(strikes, data)
    pylab.xlabel('Strike')
    pylab.ylabel('Volatility')
    pylab.legend(legends, loc = 'best', fontsize = 12)
    pylab.title(u'行权结算日: ' + str(expiries[index]), fontproperties = font, fontsize = 20)
    pylab.grid(True)

pylab.subplots(2,2, figsize = (16,14))
for i in range(1,5):
    pylab.subplot('22' + str(i))
    plotModelFitting(i-1, volSurfaces)

---

我们一直在努力

apachecn/AiLearning

---